<戻る>
このページのインデックス
論理演算基本のキ
論理演算は収集した様々な情報から欲しい情報に変換するために用い
られます。情報抽出や情報処理といってもよいでしょう。
例として、コンピュータを使う必要もないような以下のケースを考えてみます。
A.運転免許を持っているか
B.飲酒しているか
という二つの情報から、
C.運転の可否
という情報に変換する方法を考えます。
A、B及びCを以下の規則でデジタル化します。
A.免許無→0、 免許有→1
B.飲酒有→0、 飲酒無→1
C.運転不可→0 運転可→1
このとき、以下のような変換を行います。
(法律に則った答えが得られるように変換します。)
A B → C
0 0 → 0
1 0 → 0
0 1 → 0
1 1 → 1
この処理を行うにはどのような論理演算をすればよいのでしょうか。
この答えを出すため、論理演算について説明します。
最も基本的な論理演算には否定、論理和、論理積、及び、排他的論理和の4つが
あります。
・否定(NOT、反転ともいう)の演算
0 NOT = 1
1 NOT = 0
・論理和(OR)の演算
0 OR 0 = 0
1 OR 0 = 1
0 OR 1 = 1
1 OR 1 = 1
・論理積(AND)の演算
0 AND 0 = 0
1 AND 0 = 0
0 AND 1 = 0
1 AND 1 = 1
・排他的論理和(Exclusive OR,EXOR)の演算
0 EXOR 0 = 0
1 EXOR 0 = 1
0 EXOR 1 = 1
1 EXOR 1 = 0
ここで示した4つの論理演算のうち、論理積が先の例と一致していることに気付く
と思います。つまり、例で示した変換には論理積という演算を実行すればよいことが
分かった筈です。
演算対象と演算結果の関係を表にしたものを真理値表と呼びます。
例えば、ANDの真理値表を下に示します。
AND
|
A |
B |
C |
|
0 |
0 |
0 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
1 |
1 |
1 |
論理演算子
ここで示したような演算内容を示すものを演算子と呼びます。
例えば、NOT演算子などと言います。
演算対象となる値を入力値、演算した結果のことを出力値と呼ぶこともあります。
NOT : 演算対象の上に線を引いて表します。
OR : +
AND : ×
EXOR: ![]()
論理演算式
ここでは非常に簡単な例を示しましたが、これらの演算を組み合わせることで
更に複雑な演算を行うこともできます。複雑な演算を式で示すのが演算式です。
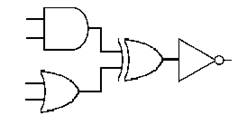
例えば、{(AとBのAND)と(CとDのOR)}のEXORの否定は次のように表記
できます。
![]()
論理回路を図示するために用いられる記号が論理回路記号です。
論理ゲートとも言います。
|
NOT |
OR |
AND |
EXOR |
NOTは○で示されます。
ここでは、バッファ記号の出力に○がついていますが、他の論理ゲートの入力や
出力に○を付けてNOTを表すこともできます。
論理回路図
論理演算の内容を論理回路記号を用いて示した図です。
実際の情報処理に関して
ここで示した例以外でも、さまざまな情報に対して適切な情報処理(論理演算)を
行えば、知りたい情報を得ることができる筈です。
ここでは、手作業でも論理演算ができるように、真理値表や演算子に関して説明
しましたが、実際の情報処理では数百万以上の入力値を扱うこともあり、現代では
殆どの人にとって真理値表や演算子を使う機会はないかもしれません。
しかし、例えば世の中には論理演算をいかに効率よく実行するかを研究している
人もいます。
どれほど演算手法が優れていても、実行するコンピュータが遅くては、答えが出
るまでに時間がかかり過ぎてしまいます。この課題解決のために、コンピュータ
の性能を改善する研究が続けられています。その研究対象がここに示したような
基本演算に相当する処理となります。
<つづく>